Model Selection of Pre-charge Resistor

Last week I met a new issue with our vehicle: pre-charge failure. The behavior was that the negative contactor and the pre-charge relay closed then open after turn on the key. After checking the whole pre-charge circuit I found that the pre-charge resistor was damaged.

Pre-charge resistor

This is the first time that a pre-charge failure has occurred, of course it caught my attention.

Principle and function

In the power system of an EV, the power battery is connected to a lot of high voltage components via PDU(Power Distribution Unit), such as the motor controller, OBC, DC-DC, A/C(Air Condition), PTC and so on. Usually in these components there are capacitor, especially in the motor controller, the capacity of capacitor could over $2000\mu F$. If the initial capacity is zero, once power on, it is equivalent to a short circuit, and the current is so large that the battery, contactor and others components will be damaged. Therefore, a pre-charge circuit is necessary for the power system to protect the main contactor, motor controller and so on.

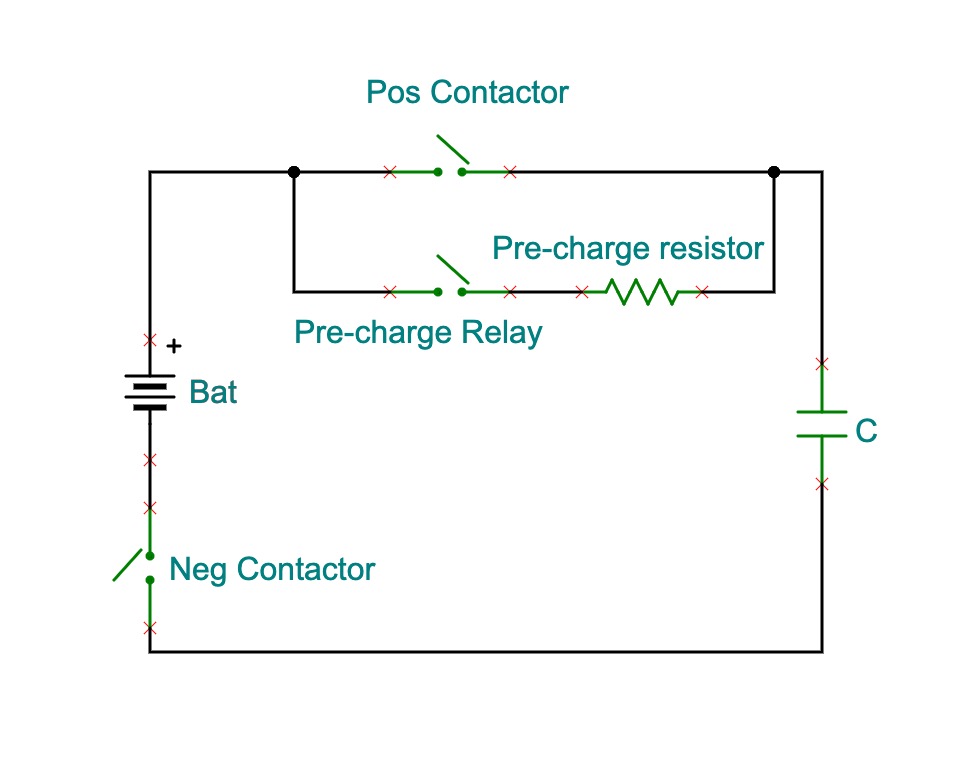Pre-charge circuit

The above is a typical pre-charge circuit, it is composed by a relay and a resistor. When the power is on, the pre-charge relay was closed before the positive contactor, and the current was limited by the pre-charge resistor. As long as the voltage of capacitor goes up to 90% ~ 95% of the battery voltage, the positive contactor will be closed and the pre-charge relay will be opened.

This is a typical first-order $RC$ series circuit. Assuming that the capacity was zero at the beginning, due to the KVL function we got:

$U_{Bat} = RC{dU_c \over dt} + U_c$

Then:

$U_c = U_{Bat} - U_{Bat}e^{-{t \over \tau}} = U_{Bat}(1 - e^{-{t \over \tau}})$

Where:

$\tau = RC$

Thus:

$t = RC, U_c = 0.63U_{Bat} \\ t = 2RC, U_c = 0.86U_{Bat} \\ t = 3RC, U_c = 0.95U_{Bat} \\ t = 4RC, U_c = 0.98U_{Bat} \\ t = 5RC, U_c = 0.99U_{Bat} \\$

At this point, it is concluded that after $3 \thicksim 5 RC$ period, the charging process is over.

Theoretical basis

For the selection of pre-charge resistor, specifically, it includes three parameters: resistance $R$, average power $P_A$, and peak power $P_P$. Others input parameters such as pre-charge time, capacitance value, and battery voltage are known.

Assuming that the voltage of power battery in full charge is $500V$, the capacitance of the capacity in motor controller is $2000\mu F$, the pre-charge time is $1s$, which is:

$t = 1s \\ C = 2000\mu F \\ V_{Bat} = 500V$

Resistance computing

According to the above equation, we stipulate that the capacity has been charged after $3RC$ time, which is:

$3RC = 1$

thus:

$R = {1 \over 3C} = {1 \over 3 * 2000 * 10^{-6} } = 166.7 \Omega$

Average power computing

The average power of the pre-charge resistor is:

$P_A = {E_C \over t}$

where $E_C = {1 \over 2}CU_C^2$, $t = 1s \, and \, U_C = U_{Bat}$.

thus:

$P_A = {E_C \over t} = {1 \over 2}CU_C^2 = 0.5 * 2000 * 10^{-6} * 500^2 = 250W$

Peak power computing

The peak power occurs when the capacitor is zero:

$P_P = {U_{Bat}^2 \over R} = {500^2 \over 166.7} = 1499.7W$

Simulation

Now let us verify the theory calculation above via a simulation model.

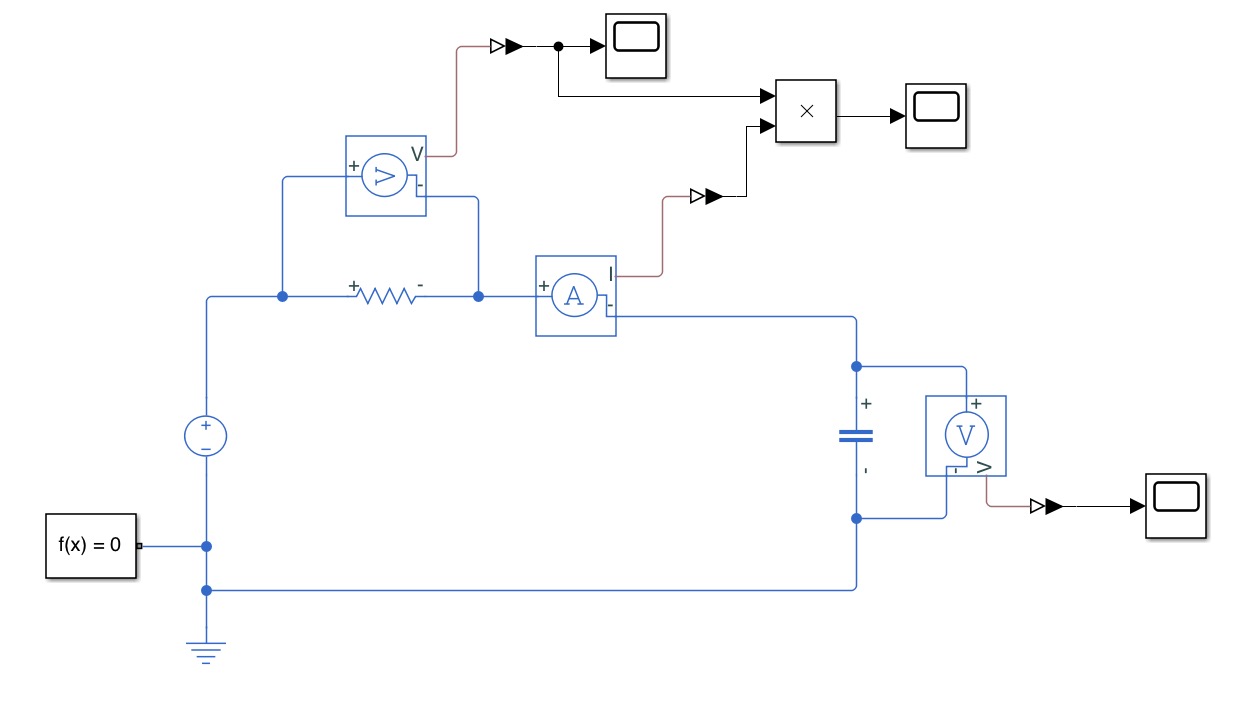Pre-charge simulation

From the simulation we got $U_C = 0.95U_{Bat}$ at $t = 1s$:

Capacitor voltage

What we have to caution is the behavior of the pre-charge resistor’s power:

Power behavior

As you can see, the peak power of the pre-charge resistor is $1497W$ while the moment the contactor closes, which verified the correction of our calculation.

Realistic basis

From the calculation we got the main parameters of the pre-charge resistor is:

$R \leqslant 166.7 \Omega, \\ P_A \geqslant 250W, \\ P_P \geqslant 1499W$

Below is a temperature rise curve from the datasheet of YAGEO pre-charge resistor:

YAGEO temperature rise curve

According to this curve, the temperature will rise up over $250^\circ C$ if a pre-charge resistor with rated power of $100W$ is at full load. Generally the pre-charge resistor is a wire-wound resistor with a ceramic shell or aluminum shell, like this:

Internal structures of a pre-charge resistor

In fact, in a very short time, the heat cannot spread via the aluminum shell or ceramic shell, it’s likes a transient pulse charging process. So the power selection for a pre-charge resistor is based on the maximum power, not the steady-state power. Usually on the datasheet, it must have the description of the peak power, for example:

YAGEO short time over load

“5 times of rated power for 5 sec”, It means we can consider the peak power with 0.2 times derating. For our example the $P_P$ will be derated to $300W$. At this point we can initially determine the model of the pre-charge resistor:

$R = 167 \Omega \\ P = 300W$

On the other hand, there is a case need to be paid much more attention which is “high frequency operation”. Imaging that someone turn the vehicle on and off repeatedly in a short time. In this case, the pre-charge resistor was at a fully loaded state for a long time, and the temperature will increased so high that the resistor could be damaged. Therefore the power of the resistor must be reserved a proper margin.

Conclusion

This article discussed the pre-charge resistor selection from the perspective of theoretical calculation. In fact, the theoretical calculation can be not only as a basis of model selection, but also used for the failure analysis. In the practical implementation, there are a lot of factors will affect the selection, and all of the experience gained in practice is very valuable.